Como descobriram que π (pi) é um valor irracional não periódico que vale aproximadamente 3,14? O estudo do cálculo do valor de pi foi realizado por Arquimedes (matemático e físico) através do método de exaustão.
Pi é uma constante que foi descoberta em razão da necessidade de calcular o comprimento de uma circunferência. Veja como Arquimedes provou o seu valor numérico:
Primeiro foi provado que todas as circunferências pertencem a um mesmo centro, portanto a razão entre o comprimento (C) de uma circunferência e o seu diâmetro (2r) será sempre igual a uma constante.
C = constante
2r
Para chegar nessa constante, Arquimedes utilizou do método de exaustão que consiste em calcular o comprimento da circunferência por aproximação, construindo polígonos inscritos e circunscritos à circunferência.
Vamos considerar C como sendo o comprimento da circunferência, 2p o perímetro do polígono inscrito (l seu lado), 2P o perímetro do polígono circunscrito (L seu lado) e r o raio da circunferência igual a 1/2.
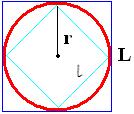
Se aumentarmos o número de lados dos polígonos acima, o comprimento da circunferência tende a coincidir com o perímetro do polígono.
Assim, podemos concluir que a razão do comprimento da circunferência pelo diâmetro está entre as razões: do 2P pelo diâmetro da circunferência e 2p pelo diâmetro da circunferência, ou seja,
2p < C < 2P.
2r 2r 2r
Arquimedes duplicou os valores dos lados do polígono até chegar a um polígono de 96 lados. Provando que 2P / 2r = 220 / 70 = 3,14286 e 2p / 2r = 223 / 71 = 3,14085, assim:
3,14085< C < 3,14286
2r
Assim a constante que representa a razão do comprimento da circunferência pelo seu diâmetro é igual a 3,14153265 .... Para facilitar os cálculos foi estipulado que essa constante seria representada pela letra grega π (pi). Portanto, a fórmula do comprimento (C) da circunferência irá ficar:
C = π
2r
C = 2 π r
Por isso que em vários problemas matemáticos que envolvem comprimento de circunferência ou área do círculo pode-se deixar os resultados em função de π ou substituí-los por 3,14.
Pi é uma constante que foi descoberta em razão da necessidade de calcular o comprimento de uma circunferência. Veja como Arquimedes provou o seu valor numérico:
Primeiro foi provado que todas as circunferências pertencem a um mesmo centro, portanto a razão entre o comprimento (C) de uma circunferência e o seu diâmetro (2r) será sempre igual a uma constante.
C = constante
2r
Para chegar nessa constante, Arquimedes utilizou do método de exaustão que consiste em calcular o comprimento da circunferência por aproximação, construindo polígonos inscritos e circunscritos à circunferência.
Vamos considerar C como sendo o comprimento da circunferência, 2p o perímetro do polígono inscrito (l seu lado), 2P o perímetro do polígono circunscrito (L seu lado) e r o raio da circunferência igual a 1/2.
Se aumentarmos o número de lados dos polígonos acima, o comprimento da circunferência tende a coincidir com o perímetro do polígono.
Assim, podemos concluir que a razão do comprimento da circunferência pelo diâmetro está entre as razões: do 2P pelo diâmetro da circunferência e 2p pelo diâmetro da circunferência, ou seja,
2p < C < 2P.
2r 2r 2r
Arquimedes duplicou os valores dos lados do polígono até chegar a um polígono de 96 lados. Provando que 2P / 2r = 220 / 70 = 3,14286 e 2p / 2r = 223 / 71 = 3,14085, assim:
3,14085< C < 3,14286
2r
Assim a constante que representa a razão do comprimento da circunferência pelo seu diâmetro é igual a 3,14153265 .... Para facilitar os cálculos foi estipulado que essa constante seria representada pela letra grega π (pi). Portanto, a fórmula do comprimento (C) da circunferência irá ficar:
C = π
2r
C = 2 π r
Por isso que em vários problemas matemáticos que envolvem comprimento de circunferência ou área do círculo pode-se deixar os resultados em função de π ou substituí-los por 3,14.
Nenhum comentário:
Postar um comentário